Chapitre CS - Pyramides, cônes et sphères
![]() Télécharger la version PDF (haute qualité).
Télécharger la version PDF (haute qualité).
Ce chapitre traite les sujets suivants:
- Pyramide
- Pyramide droite
- Cône circulaire droit (cône de révolution)
- Sphère
- Développement, aire et volume
- Pythagore dans l'espace
Il s'adresse à des classes de 9S
Apperçu
mots-clés: 9S, devoir, pyramide, volume, développement
mots-clés: 9S, pyramide, aire 3D, surface 3D
mots-clés: 9S, cône, volume, aire 3D, développement, surface 3D
mots-clés: 9S, cône, pyramide, définition
mots-clés: 9S, cône, volume, cône tronqué
mots-clés: 9S, développement, cône, volume, aire 3D, surface 3D
mots-clés: 9S, cône, volume, avancé, solide de révolution, cône tronqué

mots-clés: 9S, cône, solide de révolution, aire 3D, surface 3D
Textes
Exercice GMO-CS-1
Mots-clés: 9S, devoir, pyramide, volume, développement
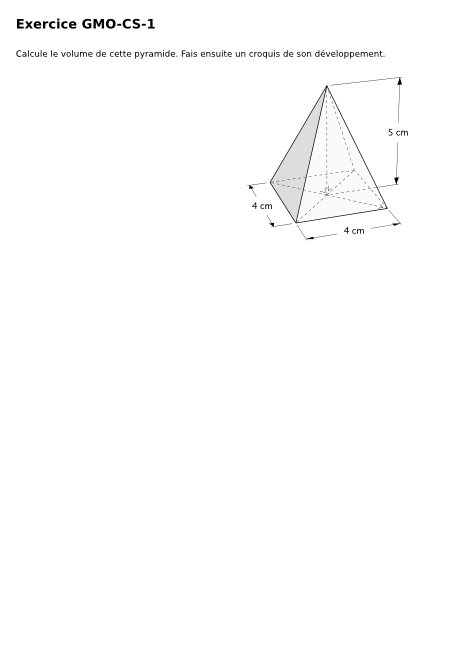
Calcule le volume de cette pyramide. Fais ensuite un croquis de son développement.
Exercice GMO-CS-2
Mots-clés: 9S, pyramide, aire 3D, surface 3D
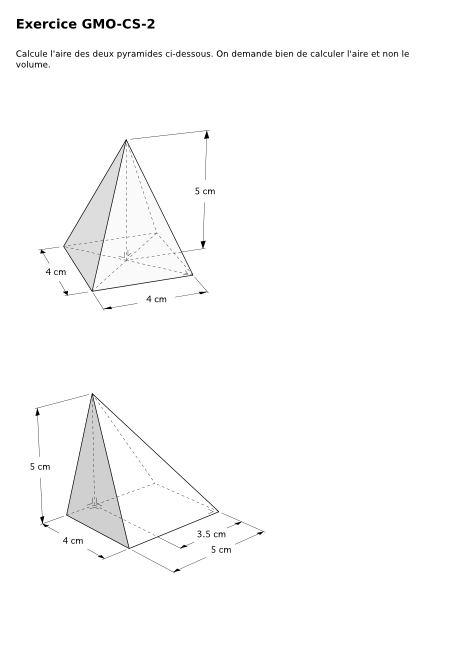
Calcule l'aire des deux pyramides ci-dessous. On demande bien de calculer l'aire et non le volume.
Exercice GMO-CS-3
Mots-clés: 9S, cône, volume, aire 3D, développement, surface 3D
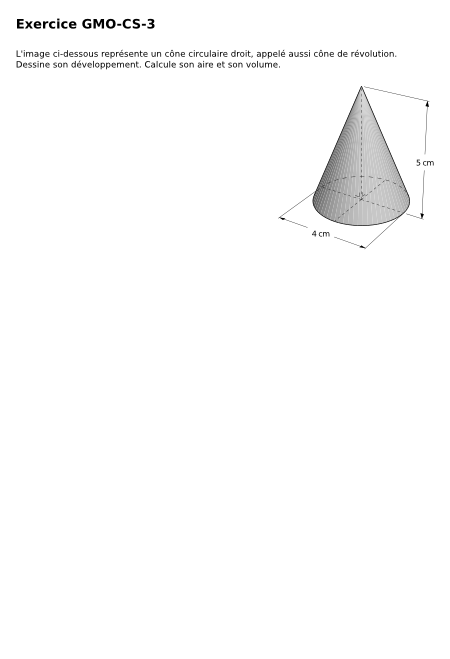
L'image ci-dessous représente un cône circulaire droit, appelé aussi cône de révolution. Dessine son développement. Calcule son aire et son volume.
Exercice GMO-CS-4
Mots-clés: 9S, cône, pyramide, définition
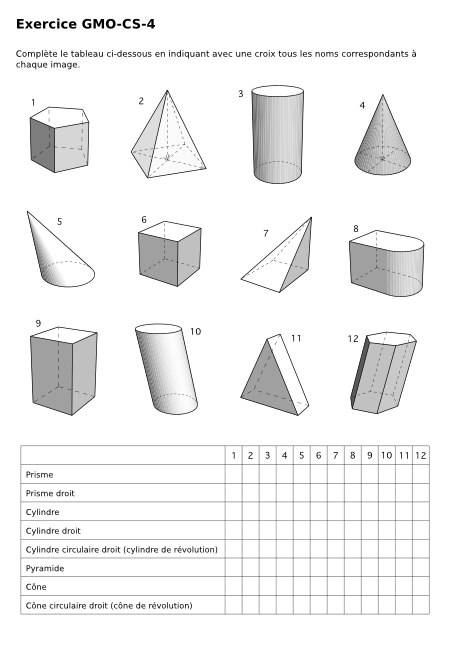
Complète le tableau ci-dessous en indiquant avec une croix tous les noms correspondants à chaque image.
Prisme
Prisme droit
Cylindre
Cylindre droit
Cylindre circulaire droit (cylindre de révolution)
Pyramide
Cône
Cône circulaire droit (cône de révolution)
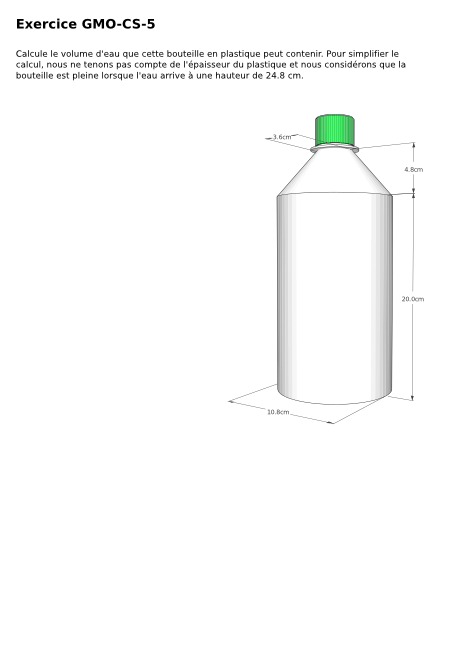
Exercice GMO-CS-5
Mots-clés: 9S, cône, volume, cône tronqué
Calcule le volume d'eau que cette bouteille en plastique peut contenir. Pour simplifier le calcul, nous ne tenons pas compte de l'épaisseur du plastique et nous considérons que la bouteille est pleine lorsque l'eau arrive à une hauteur de 24.8 cm.
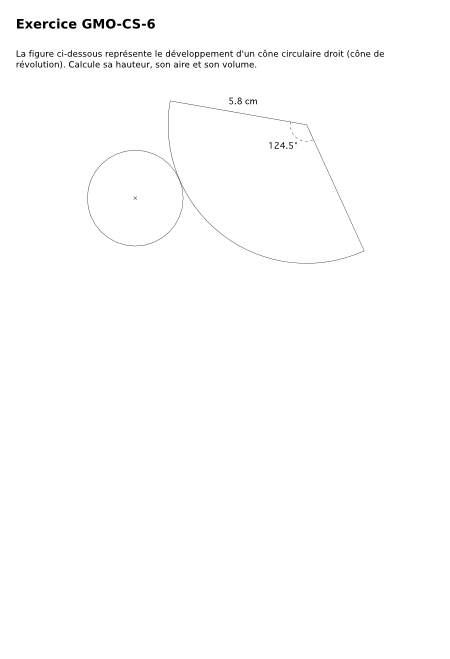
Exercice GMO-CS-6
Mots-clés: 9S, développement, cône, volume, aire 3D, surface 3D
La figure ci-dessous représente le développement d'un cône circulaire droit (cône de révolution). Calcule sa hauteur, son aire et son volume.
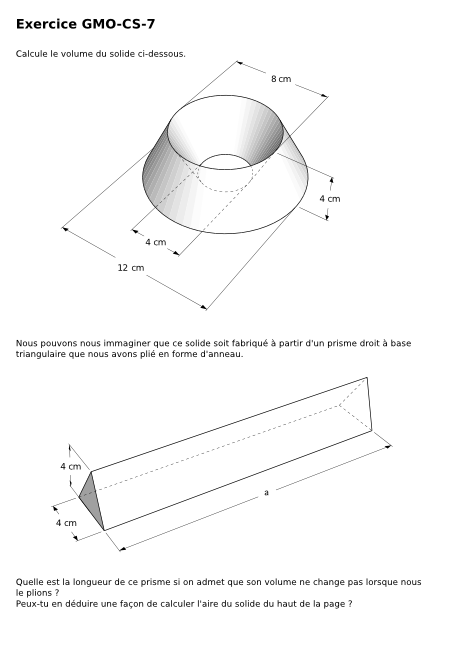
Exercice GMO-CS-7
Mots-clés: 9S, cône, volume, avancé, solide de révolution, cône tronqué
Calcule le volume du solide ci-dessous.
Nous pouvons nous immaginer que ce solide soit fabriqué à partir d'un prisme droit à base triangulaire que nous avons plié en forme d'anneau.
Quelle est la longueur de ce prisme si on admet que son volume ne change pas lorsque nous le plions ?
Peux-tu en déduire une façon de calculer l'aire du solide du haut de la page ?
Exercice GMO-CS-8
Mots-clés: 9S, cône, solide de révolution, aire 3D, surface 3D
J'aimerais fabriquer un tipi comme celui illustré dans la photo. Je peux assimiler cette tente à un cône de 3m de diamètre et 3m de hauteur. Quelle est la surface de toile dont j'ai besoin ? Quelle forme devra-t-elle avoir (rayon, angle) ? Pour simplifier mes calculs, je ne tiens compte ni de la porte, ni de l'ouverture du haut.
Copyright 2005 Immanuel Giel, GFDL, http://fr.wikipedia.org/wiki/Fichier:Karl_May_Museum_Tipi.jpg